今回は、ルンゲクッタ法を用いて、サインカーブを計算してみました。
ローレンツアトラクタとかトーマスアトラクタとか描画してみたいなーと思って、ひとまず手始めにルンゲクッタ法を使えるようになろうと思ってやってみました。
ルンゲクッタ法についてはまだまだ分かってない部分はあるものの、オイラー法の拡張って感じですかね。
4次のルンゲクッタ法を使えば、かなり正確に数値解析をできるようです。
ルンゲクッタ法にもまぁ色々あるようですが、今回は4次のルンゲクッタ法(古典的ルンゲクッタ法)を使いました
$$
\begin{eqnarray}
&&y’=f(t,y),y(t_0)=y_0\\
&&y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)\\
&&t_{n+1}=t_n+h\\
\\
&&k_1=f(t_n,y_n) \cr
&&k_2=f(t_n+\frac{h}{2},y_n+\frac{h}{2}k_1)\cr
&&k_3=f(t_n=\frac{h}{2},y_n+\frac{h}{2}k_3)\cr
&&k_4=f(t_n+h,y_n+hk_3)
\end{eqnarray}
$$
こんな感じのことをプログラムしていきます。
ルンゲクッタ法を計算する関数をこんな感じに書いてみました。
fn rk4<F:Fn(f64,f64)->f64>(f:F,x:f64,y:f64,h:f64)->f64{
let k1 = f(x,y)*h;
let k2 = f(x + 0.5*h,y+0.5*k1)*h;
let k3 = f(x + 0.5*h,y+0.5*k2)*h;
let k4 = f(x+h,y+k3)*h;
return y+(k1+2.0*k2+2.0*k3+k4)/6.0;
}関数を引数にする関数で、使えるように
これで実際にサインカーブを描いてみましょう。
描画にはrustのnannouを使っています。
use nannou::prelude::*;
pub fn main() {
nannou::app(model).update(update).run();
}
const DELTA:f64 = 0.01;
struct Model {
_window: window::Id,
px:f64,
py:f64,
}
fn model(app: &App) -> Model {
let _window = app
.new_window()
.view(view)
.key_pressed(key_pressed)
.mouse_pressed(mouse_pressed)
.build()
.unwrap();
Model { _window,
px:0.0,
py:0.0,
}
}
fn update(_app: &App, m: &mut Model, _update: Update) {
m.py = rk4(f1,m.px,m.py,DELTA);
m.px +=DELTA;
}
fn view(app: &App, m: &Model, frame: Frame) {
let draw = app.draw();
if frame.nth() == 0 || app.keys.down.contains(&Key::R) {
draw.background().color(BLACK);
}
let x = 50.0*(m.px as f32)-300.0;
let y = 100.0*(m.py as f32);
draw.line()
.points(pt2(-400.0,0.0),pt2(400.0,0.0))
.weight(2.0)
.color(WHITE);
draw.line()
.points(pt2(-300.0,200.0),pt2(-300.0,-200.0))
.weight(2.0)
.color(WHITE);
draw.ellipse()
.x_y(x,y)
.radius(5.0)
.color(WHITE);
draw.to_frame(app, &frame).unwrap();
}
fn f1(x:f64,y:f64)->f64{
x.cos()
}
fn rk4<F:Fn(f64,f64)->f64>(f:F,x:f64,y:f64,h:f64)->f64{
let k1 = f(x,y)*h;
let k2 = f(x + 0.5*h,y+0.5*k1)*h;
let k3 = f(x + 0.5*h,y+0.5*k2)*h;
let k4 = f(x+h,y+k3)*h;
return y+(k1+2.0*k2+2.0*k3+k4)/6.0;
}
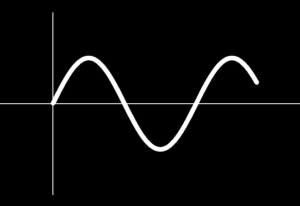
こんな感じで、描くことができました。
他にも条件式を変えると
$$y=x^4-2x^3+1\\y’=4x^3-6x^2$$
っていう4次式のグラフも計算してみると
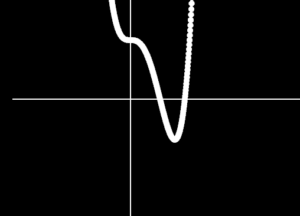
こんな感じに概形がとれていて、おそらくあってます。
これを活用して、ローレンツアトラクタやトーマスアトラクタとか計算して、描画していく予定です。



コメント