juliaでルンゲクッタ法を実装して、ローレンツアトラクタを描画してみました。
ルンゲクッタ法の解説については、以前rustで実装したので、そちらをご覧ください
Rustで作ったルンゲクッタ法のソースコードをそのまま、juliaに移植した感じです。
今回は、1階3連立の常微分方程式を計算するようにしたので、ソースは長く見えますが、同じことの繰り返しをしているだけです。
4次のルンゲクッタ法のアルゴリズム
juliaの4次のルンゲクッタ法(Runge-Kutta)のアルゴリズムこんな感じです。
$$
\begin{eqnarray}
&&y’=f(t,y),y(t_0)=y_0\\
&&y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)\\
&&t_{n+1}=t_n+h\\
\\
&&k_1=f(t_n,y_n) \cr
&&k_2=f(t_n+\frac{h}{2},y_n+\frac{h}{2}k_1)\cr
&&k_3=f(t_n=\frac{h}{2},y_n+\frac{h}{2}k_3)\cr
&&k_4=f(t_n+h,y_n+hk_3)
\end{eqnarray}
$$
これをjuliaのソースコードに起こし込んでいきます。
function rk4(t,x,y,z,h)
k1x = fx(t, x, y, z) * h
k1y = fy(t, x, y, z) * h
k1z = fz(t, x, y, z) * h
k2x = fx(t + 0.5 * h,x + 0.5 * k1x,y + 0.5 * k1y,z + 0.5 * k1z) * h
k2y = fy(t + 0.5 * h,x + 0.5 * k1x,y + 0.5 * k1y,z + 0.5 * k1z) * h
k2z = fz(t + 0.5 * h,x + 0.5 * k1x,y + 0.5 * k1y,z + 0.5 * k1z) * h
k3x = fx(t + 0.5 * h,x + 0.5 * k2x,y + 0.5 * k2y,z + 0.5 * k2z) * h
k3y = fy(t + 0.5 * h,x + 0.5 * k2x,y + 0.5 * k2y,z + 0.5 * k2z) * h
k3z = fz(t + 0.5 * h,x + 0.5 * k2x,y + 0.5 * k2y,z + 0.5 * k2z) * h
k4x = fx(t + h, x + k3x, y + k3y, z + k3z) * h
k4y = fx(t + h, x + k3x, y + k3y, z + k3z) * h
k4z = fz(t + h, x + k3x, y + k3y, z + k3z) * h
nx = x + (k1x + 2.0 * k2x + 2.0 * k3x + k4x) / 6.0
ny = y + (k1y + 2.0 * k2y + 2.0 * k3y + k4y) / 6.0
nz = z + (k1z + 2.0 * k2z + 2.0 * k3z + k4z) / 6.0
return nx,ny,nz
end
ローレンツ方程式は次のように与えます。
function fx(t,x,y,z)
a*(-x+y)
end
function fy(t,x,y,z)
-x*z+b*x-y
end
function fz(t,x,y,z)
x*y-z*c
endローレンツ方程式を計算していく
ルンゲクッタ法のアルゴリズムとローレンツ方程式を実装できたので、これを計算してきます。
計算を実行する関数を作る
計算する関数を作ります。
nが回数、dが刻み幅、icが初期条件
function rungekutta(n,d,ic)
t=0.0
x0,y0,z0=ic
x=[x0]
y=[y0]
z=[z0]
for i=1:n
nx,ny,nz = rk4(t,x[i],y[i],z[i],d)
push!(x,nx)
push!(y,ny)
push!(z,nz)
t=t+delta
end
return x,y,z
endforループを使って、繰り返し計算して、結果をそれぞれ収納していきます。
実際に計算する
係数をa=10,b=28,c=8/3として、初期値をx=1.1,y=0.5,z=0.5とします。
刻み幅を0.001、計算回数を100,000回としましょう
using Plots
a = 10.0
b=28.0
c =8/3
function main()
ic = (1.1,0.5,0.5)
x,y,z =rungekutta(100000,0.001,ic)
plot(x,y,z)
endこれで、main関数を実行すると、計算を実行して、グラフ描画してくれます。
描画する
描画は今回は、Plots.jlを使って描画してます。
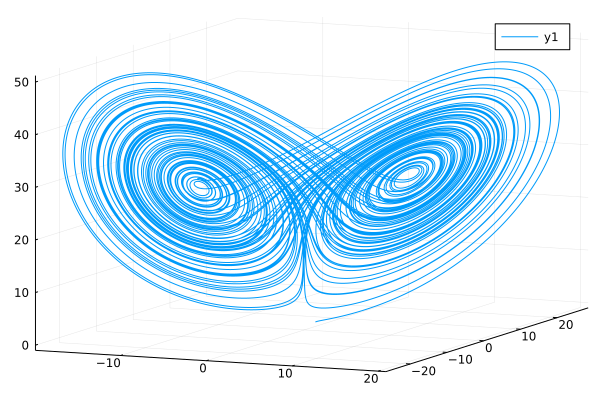
まとめ
今回は、juliaで4次のルンゲクッタ法のアルゴリズムを実装して、ローレンツ方程式を計算して、描画してみました。精度よく、計算できているんじゃないでしょうか?
juliaには、DifferentialEquations.jlっていう常微分方程式を計算するパッケージがあります。これを使うと結構簡単に計算することができます。
今回プログラムは50行ぐらい書きましたが、パッケージを使えば15行ぐらいのソースで計算できます。
自分で実装してみるのは、向学のためにはいいのかななんて(笑)

コメント