Rust Nannouで振り子を再現してみましょう。
糸の先におもりがついてて、それがゆーらゆーら左右に揺れる、アレです。
ではやっていきましょう!
振り子の運動方程式
振り子の動きを計算するために振り子の運動方程式を求めましょう。
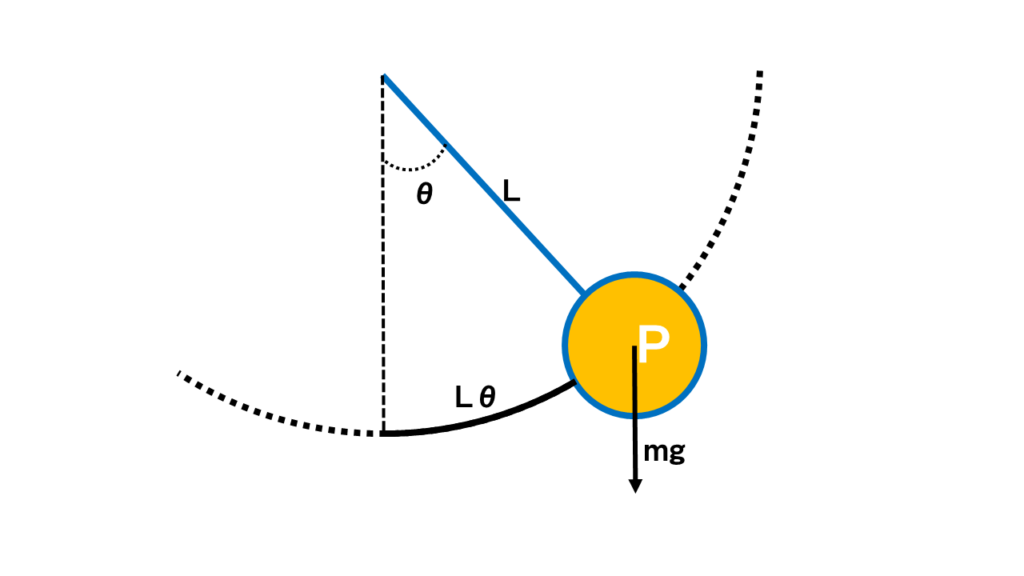
振り子(P)の動きはこんな感じね。
紐があって、おもりがあって、それが、円運動する感じです。
Pの円弧に係る動きを元にPの速度(v)を表すと$$v=L\frac{d\theta}{dt}$$となるから、加速度(a)は、さらにそれを微分して$$a=L\frac{d^2\theta}{dt^2}$$となる。
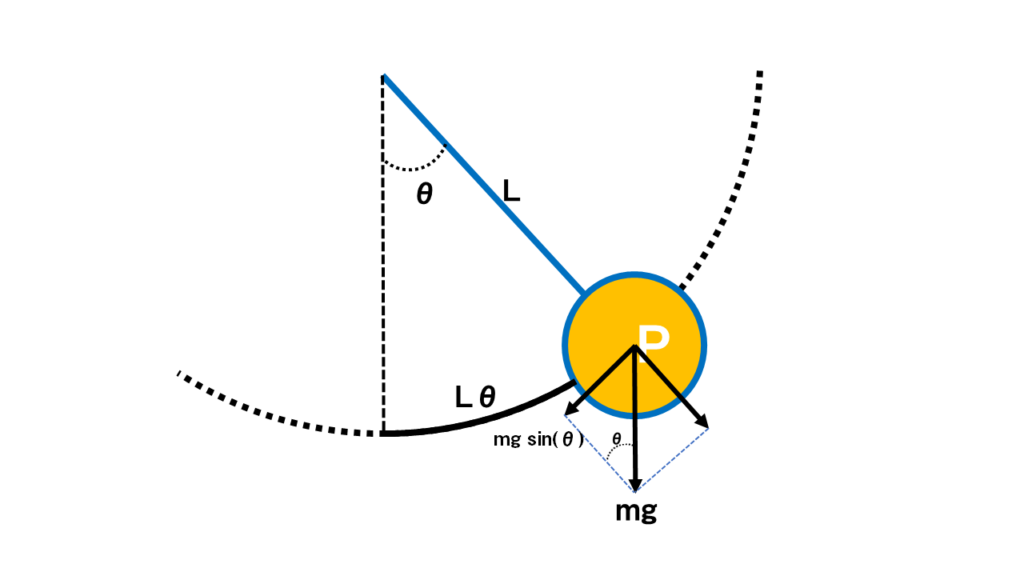
おもりPの円に沿って動く方向に働く運動方程式(\(F=ma\))を考えると$$F=-mg\sin(\theta)$$となるので
さっきの最初の加速度の式と合わせると$$mL\frac{d^2\theta}{dt^2}=-mg\sin(\theta)$$となる。
でちょっと整理して$$\frac{d^2\theta}{dt^2}=-\frac{g}{L}\sin(\theta)$$となる。
この\(\displaystyle\frac{d^2\theta}{dt^2}=-\frac{g}{L}\sin(\theta)\)が瞬間あたりのθの変化速度の変化量なので、これをプログラムで再現するときに使います。
もっと厳密な話は、本を読んだり、ネット検索をして調べてください。ここでは、あくまでrust nannouで振り子を表現するのに必要な程度しか触れてません。
運動方程式をプログラムしていく
では、さっき作った運動方程式を元にRust nannouで振り子をプログラミングしていきましょう。
ザックリどんなプログラムをしていくかって言うと、さっき求めた瞬間当たりの角度θの変化を積分して積分して元々の角度を割り出して、それをもとに描画する感じです。
ここでいう積分ってのは、前もやりましたが、インクリメントです。
なんだそりゃ?という方は、こちらの記事を読んでみてください。
変数を準備していく
振り子描画で使う変数を準備していきましょう。
struct Model {
origin: Vector2,
theta: f32,
furiko_a: f32,
furiko_v: f32,
len: f32,
g: f32,
}こんな感じですね。
originは原点です。振り子を吊り下げる点を指定するために使ってます。(別にModelに定義しなくてもいいんじゃないか疑惑)
thetaは角度ですね。
furiko_aは角度の速度の変化量\(\displaystyle\frac{d^2\theta}{dt^2}=-\frac{g}{L}\sin(\theta)\)これを計算して収納するために使います。
furiko_vこれが角度の速度。
lenは振り子の長さ
gは重力加速度
これをmodel関数の中で次に初期化していきます。
fn model(app: &App) -> Model {
...
...
Model {
origin: pt2(0.0, 300.0),
theta: PI / 3.0,
furiko_a: 0.0,
furiko_v: 0.0,
len: 400.0,
g: 1.0,
}
}thetaの初期の場所を指定します。これ、ゼロとかにしちゃうと動かないので(笑)ご注意ください。
ゼロにしてて外力が無くて動き出したら、世の中のブランコは全部ポルターガイストが起こっちゃう。
運動方程式を計算してthetaを求める
運動方程式を計算して、角度thetaを求めていきましょう。
先述したように、今回は角度の速度の変化量を考えたので、それを積分して角度を求めていきます。
まずは、変化量(furiko_a)\(\displaystyle\frac{d^2\theta}{dt^2}=-\frac{g}{L}\sin(\theta)\)を計算して、
それをインクリメントして速度(furiko_v)を求めます。
そして、速度(furiko_v)をインクリメント角度(theta)を求めていきます
では、コードを書いていきましょう。
update関数の中に書いていきます
fn update(_app: &App, model: &mut Model, _update: Update) {
model.furiko_a = (-1.0) * model.theta.sin() * model.g / model.len;
model.furiko_v += model.furiko_a;
model.theta += model.furiko_v;
}これでtheta計算することができました。
次は描画です
求めたthetaから描画する
描画は、求めたthetaの値を使って、座標を計算していきます。
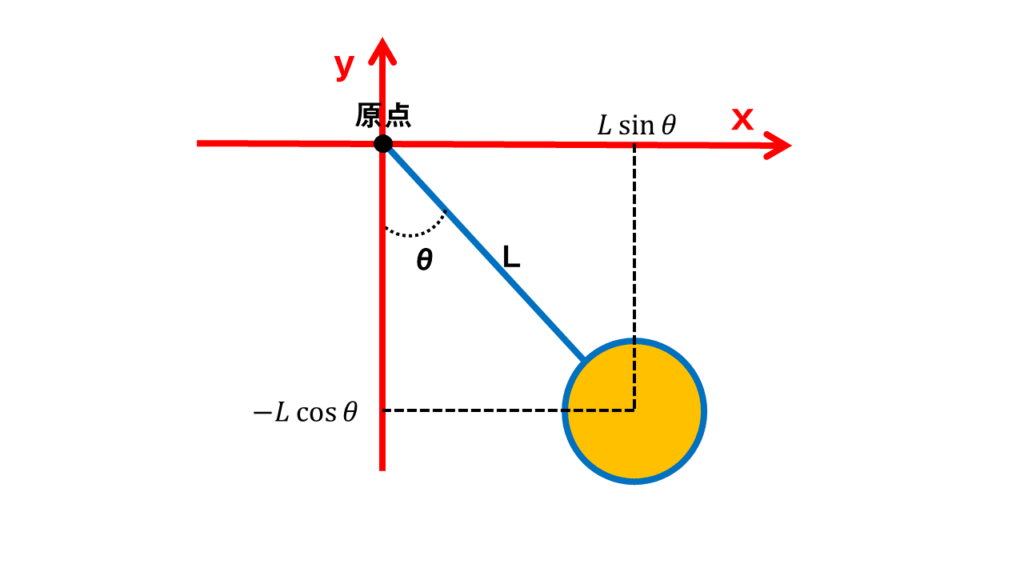
三角関数を使って、振り子の長さとthetaを使って、素直に計算
この図は原点からですが、今回は原点の位置をずらすので、平行移動分を座標に足します。
座標を計算するソースコードはこんな感じ
let x = model.theta.sin() * model.len + model.origin.x;
let y = -model.theta.cos() * model.len + model.origin.y;originが原点の平行移動分。
あとは、天井と振り子の棒とおもりを描画部分
//天井
draw.line()
.points(pt2(-300.0, model.origin.y), pt2(300.0, model.origin.y))
.weight(5.0)
.color(WHITE);
//振り子の棒
draw.line()
.points(model.origin, pt2(x, y))
.weight(3.0)
.color(WHITE);
//振り子のおもり
draw.ellipse().x_y(x, y).radius(50.0).color(WHITE);こんな感じですね。
これで、振り子を描画することができました。
まとめ
今回は、rust nannouを使って振り子を描画しました。運動方程式を求めて、そこから変化量を積分してと、いろいろなことを応用した感じですね。
二重振り子とか三重振り子とかだと軌跡がカオスになったりと面白いのでジェネラティブアートに活用できるかもしれませんね。
今回のインクリメントとかの考え方を使えば、振り子以外にもいろんなものの動きの描画に役立ちますので、是非試してみてくださいね。
ではまた



コメント