juliaでSudokuを解く

今回は、juliaでSudoku(Number Place)を解きます。

Sudokuを解くアルゴリズムは色々ありますが、今回は、深さ優先探索っていうの？再帰を使った解法（一番単純？）なやつでやっていきます。

Sudokuのルール
Sudokuを解くアルゴリズム
Juliaで実装
1. Sudokuのデータを保管する
2. 空白を探す
どんな数字が入るか調べる関数
1. 数字を入れて解を進めていく関数
まとめ

Sudokuのルール

Sudokuは、9×9の盤面に1から9の数字を入れていくパズルです。

ルールは、縦・横、3×3の枠内のマスに１から9の数字を一つずつ入れる。

とっても簡単なルールです。

Sudokuを解くアルゴリズム

Sudokuを解くアルゴリズムを考えていきましょう。

今回実装するアルゴリズムは、人が、Sudokuを解くのとほぼ同じ手順を踏んでいきます。

空いた枠を見つける
空いた枠にどんな数字が入るか探す
可能性のある数字を入れてみて、進めてみる
ダメだったら、違う数字を入れてみる
全部埋まるまで、２，３，４の作業を繰り返す
全部埋まったら終わり。

Juliaで実装

Juliaで今考えたアルゴリズムを実装していきましょう。

アルゴリズムから次の3つの関数を作って、解いていきます。

空白を探す関数
どんな数字が入るか調べる関数
数字を入れて解を進めていく関数

Sudokuのデータを保管する

関数を定義して、解いていく前にSudokuのデータ表現をします。

Sudokuは9×9のマス目になってますので、処理するときに便利なように行列で保存しておきます。

juliaだと素直に行列を書けば、行列として保存できるので、やっていきましょう。

grid = [4 0 0 0 0 7 0 0 8;
        0 0 0 0 0 0 0 1 0;
        0 0 2 0 3 0 5 0 0;
        0 0 0 0 0 8 0 0 7;
        0 5 3 0 0 0 0 9 0;
        0 0 0 0 0 4 0 0 0;
        0 0 0 0 6 0 0 0 0;
        0 0 0 0 5 0 0 3 0;
        8 0 0 0 0 0 0 0 0;]

最初から数字の入っているところにはその数字を入れます。空白の部分は０で埋めます。

要素の指定方法は、

grid[行,列]

例えば、1行6列目の要素は7

grid[1,7]

これでアクセスできます。

ここから先の解説では、行は縦なのでｙ、列は横なのでxとして、表記していきます。

grid[y,x]

こういう感じで使います。

空白を探す

実際に数字を入れていくセル、空白（ゼロ）を探す関数を定義していきましょう。

問題データを渡したら、空白の座標（ｘ、ｙ）を返値として返してくる関数を考えます。

もし、空白が無ければ-1をそれぞれ返します。

function find_cell(grid)
    for y=1:9, x = 1:9
        if grid[y,x] == 0
            return x,y
        end
    end
    return -1,-1
end

ひたすら上から順番にループ回して、探してくるっていう感じです。

juliaのforループでは、多重ループをする時に

for i=1:9
    for j=1:9
      処理
    end
end

とは書かずにfor一本で書けるのでスッキリします。

for i=1:9,j=1:9
    処理
end

上も下も同じ結果が返ってきます。

どんな数字が入るか調べる関数

空白が見つかったので、そこに数字を入れますが、どんな数字が入れれるのか調べる必要があります。

今入っている数字を被らないのを見つけないといけないです。

調べるのは、縦、横、3×3の枠内の3つについてです。

まずはコードを見てみましょう

function possible(x,y,n,grid)

#y方向でチェック
    for i in 1:9
        if grid[i,x] == n
            return false
        end
    end

#x方向のチェック
    for i in 1:9
        if grid[y,i] ==n
            return false
        end
    end

#3x3マスのチェック
    yo = div(y-1,3)*3
    xo= div(x-1,3)*3
    for i = 1:3,j =1:3
        if grid[yo+i,xo+j] == n

            return false
        end
    end

    return true
end

上から順番にy方向、x方向、3×3マス内のチェックと進んでいきます。

引数で座標（ｘ、ｙ）と数字（ｎ）を渡してます。渡した座標にｎが入るかどうかを調べてます。

上の2つのは、単純にそれぞれの方向に進めていけば、チェックできます。

3×3マスは、3×3マスを取り出してこないとチェックできません。

そこで、9×9マスの座標と3×3マスの座標を変換して処理をする必要があります。

3×3マスの起点になる座標を計算するのが最初の2行です。

yo = div(y-1,3)*3
xo = div(x-1,3)*3

Sudokuを解くプログラムのサイトをいくつか見て参考にしたときに、3で割って整数部を見ればOKですよってことでした。

pythonの場合、添え字が０，１，２，３，４，５，６，７，８となっています。すると、０，１，２を3で割ると整数部は０，同様に４，５，６は１，６，７，８は２となって、そこに３を掛けると元の座標と3×3の座標の変換ができちゃうっていう優れものです。

Juliaの場合は、添え字が１からスタートで、１，２，３，４・・・となっています。そこで、座標を1引いて計算することで、同じように処理できるようにしています。

for文の中は、単純にループを回して、与えたｎが入るかどうか調べています。

数字を入れて解を進めていく関数

空白のチェック、数字が入るかどうか調べる関数ができたので、実際に数字を入れて解を進めていく関数を作っていきましょう。

function solv(x,y,grid)
    x,y = find_cell(grid)
    if  x==-1
        return true
    end

    for n =1:9
        if possible(x,y,n)
            grid[y,x]=n
            if solv(x,y)
                return true
            end

            grid[y,x]=0
        end
    end
    return false
end

パートごとに見ていきましょう

x,y = find_cell(grid)
if  x==-1
    return true
end

まずは、空白セルを探します。もし、‐1が返ってきたら、空白なし＝解が求められているということで、trueを返して関数から抜けます。

for n =1:9
    if possible(x,y,n)
       grid[y,x]=n
       if solv(x,y)
            return true
       end
            grid[y,x]=0
    end
end

possible関数を使って、空白セルに対して、数字ｎが入るかどうか調べます。

もし入るのであれば、その数字を入れてみます。

次のif文でそれをもう一度自身の関数を呼び出します。

このif文がfalseであれば、その座標は0に戻して、やり直します。それを繰り返して、解を求めていきます。

まとめ

実際に解いてみると、簡単なものから超難問みたいなものまで、解を求めることができました。

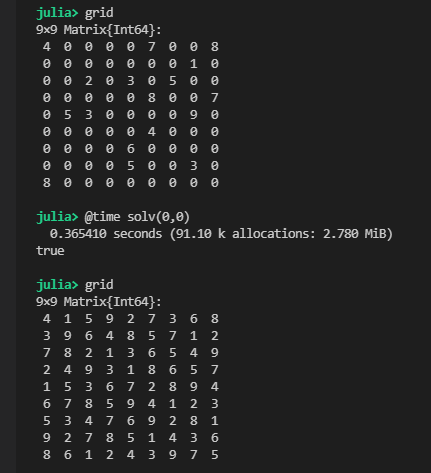
簡単な問題は本当0.02秒とかで求めることができます。一瞬です。ただ、難易度が上がると時間がかかります。これは、単純な解き方ゆえの問題点でしょう。

実際人が解くときは、まずは当てはめやすいところをやって、そして、入る数字のリストを作って・・・と効率的に解いていくところ、今回のアルゴリズムの場合は、もう力業ですから、効率もくそもなく、時間がかかるのは仕方がないです。

数独を解くアルゴリズムは他にもいくつかあるので、他のものも実装してみるも楽しいと思います。

是非チャレンジしてください