$$\int$$
こんな記号覚えてますか?
高校のころにちょっとだけ出てきた、積分の記号ですね。
今回は、rustで定積分を計算してみましょう。
定積分を計算しよう
積分は不定積分と定積分ってのがあったんですが、今回は定積分を計算していきます。
$$\int_{0}^{1}(3x^2+2)dx$$
を例にやっていきましょう。
定積分と区分求積法
今回、rustで定積分を計算するときは、「区分求積法」をヒントにやっていきます。
定積分と区分求積法ではこんな関係がありました。
$$\lim_{n \to \infty}\frac{1}{n}\sum_{k=1}^{n}f\Bigl(\frac{k}{n}\Bigl)=\int_{0}^{1}f(x)dx$$
これですね。

ザックリ言うと、細かーく分割して、それを足し合わせれば全体になるじゃんってこと
rustで書いてみましょう
では、定積分は区分求積法すればいいってことなので、素直にこれをプログラミングしてみましょう。
やることは、2つ。
細かく分割して、足し合わせる
次の式を例にやっていきましょうね
$$\int_{0}^{1}(3x^2+2)dx$$
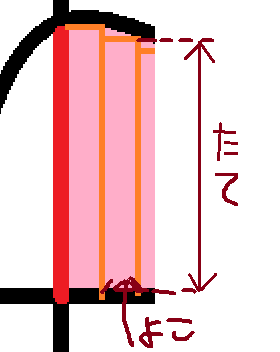
細かく分割

オレンジの枠で分割されたものが細分化した一つ一つです。これの面積を足し合わせるっていう作業をしていくとイメージしてください。
四角形の面積は、縦かける横。
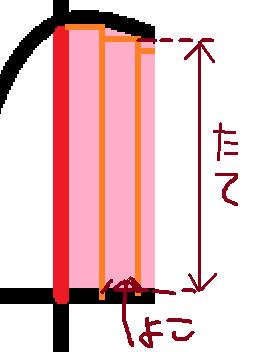
縦は、関数\(f(x)\)のxに値を入力した結果です。
横は細分化するための条件です。ここではdelta_xとしましょう。
足し合わせる
足し合わせるをプログラムで考えるときは、「インクリメント」です。
let mut s:f64 = 0.0; //初期値
s += hogehoge; //足していく内容rustで書くとこんな感じですね。
rustの場合は、mutをつけておかないと、変数の内容を書き換えれないので、注意。
rustを使った定積分
1,2を踏まえて、次の積分を求めるソースを書いていきましょう。
$$\int_{0}^{1}(3x^2+2)dx$$
fn main(){
//初期値の設定とか
let delta_x:f64 = 0.01;
let mut s:f64 = 0.0;
let mut x:f64 = 0.0;
//細かくして足す作業
while x<=1.0{
s += (3.0*x.powi(2)+2)*delta_x;
x += delta_x;
//結果を出力
println!("{:?}",s);
}3行目のdelta_xはどれぐらい細分化するかの設定。この場合0.1刻みで分割します。
図のヨコに相当する部分です。
積分範囲は0から1なので、xの初期値はゼロです。
もし3から5とかだったらxは3からスタート。
7行目のwhile文の条件x<=1.0これが積分範囲の終点。
8行目が細かくして足す作業。
まずは、長方形の面積だから、縦かける横。
縦は(3.0*x.powi(2)+2)、横はdelta_x
それをs+=でインクリメント。
最後に出力。
実際の計算結果。
この定積分。
普通に公式に入れてとくと、答えは3。
コンピュータで計算すると。おそらく3っていう決まった数字にはならないと思います。
僕のPCで計算すると変数がf64だと2.9850500000000024っていう値が出ました。
f32だと3.0350492っていう値です。
なぜかっていうと、コンピュータは、細かく分割して足すっていう計算を繰り返したので、微妙な誤差が出てしまいます。その誤差の分ずれてるってことです。
近似と誤差
え!そしたら、意味ないじゃん!?不正確じゃん!?って思うかもしれません。
たしかにこの程度の積分だと「え!」ってなるかもしれませんがもっと複雑になればそもそも無限に続く数に対して大体の近似をしてくことになります。
例えば、積分結果が\(2\log5+7\sqrt2\)とかなったらどうでしょう?これを見たらパッと計算できないですよね?コンピュータはこれをある程度計算して近似値を出してくれます。そこにはもちろん誤差も含まれます。
誤差がある。それが普通なんです。それをどういう風に考えるか?が大切です。
なにも近似や誤差はコンピュータだけではありません。僕らだって、例えば円の面積(半径かける半径かけるPI)の計算は正確にはできません。PIが無限に続く少数だから、3.1415・・・ってね。どっかで切る捨てるでしょ?
なので、世の中近似と誤差ばかり(笑)逆に正確に値がピタッと決まるほうが珍しいかもしれませんね。
まとめ
今回は定積分をrustで解いてみました。
考え方は、区分求積法でしたね。細かく分けて足す。
プログラムでこれがどこで役立つの?って思う人もいると思いますが、それはまた、別の記事で紹介していきます。
ではまたね!


コメント
[…] […]
[…] […]