ピンボールやブロック崩しなど、ステージ内でボールが跳ね返るゲームってありますよね。
そういう跳ね返るボールを今回はRust nannouで描画していきたいと思います。
動くボールを描画する
跳ね返るボールを描画する前に、まずは、動くボールを描画していきましょう。
ボールが動くっていうのは、時間毎に座標を少しずつ変化させて、それを描画していく処理です。
Modelにボールの情報を定義する
では、Modelにボールの情報を定義してきましょう。
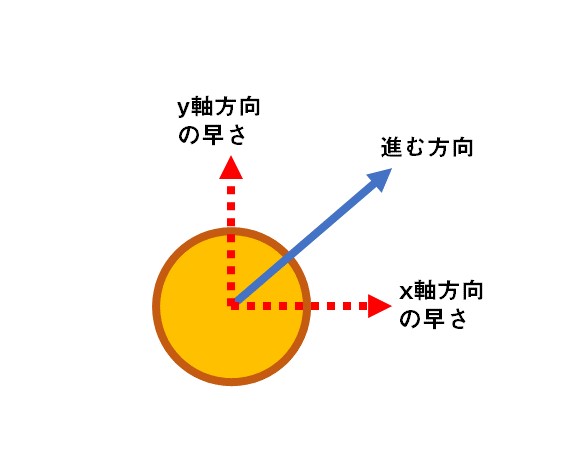
動くボールは、位置(座標)と速度(向きと速さ)の情報を持っています。
ボールの座標(px,py)速度(vx,vy)とします。
速度は、早さだけではなく、向きの情報も必要なので、vx,vyとして、x向きの速さ、y向きの早さというようにしておきます。
struct Model{
px:f32,
py:f32,
vx:f32,
vy:f32,
}ボールの情報の初期化と更新
ボールの情報をまずは初期化して、そのあと、更新する作業を繰り返していきます。
初期化
structでModelが作れたら、まずは初期化しましょう。
fn model(app: &App) -> Model {
...
...
let px = 0.0;
let py = 0.0;
let vx = 1.0;
let vy = 1.0;
Model{
px,
py,
px,
vy,
}
}まずは、スタートは原点。速度はそれぞれ1.0としましょう。
情報の更新
次に情報を更新していくことで、座標を変化させて、ボールを移動させていきます。
移動した位置は、速度の積分で表現できます。
ここでいう積分は、微小量の足し合わせ、インクリメントです。
ソースコードはこんな感じです
fn update(app: &App, model: &mut Model, _update: Update) {
let speed = 2.0;
model.px += speed * model.vx;
model.py += speed * model.vy;
}こんな感じです。
今回vx,vyはどちらかというと加速度のような役割、speedが速さを表すような役割にしています。
かけ合わせて足し合わせていきます。
理科・物理で速度や物体の位置についてこんな公式習いましたよね。
$$v_t=v_0+at$$
$$\begin{eqnarray}
x=\int v_0 + at dt \\
=v_0t+\frac{1}{2}at^2+c
\end{eqnarray}$$
このプログラムではこれを疑似的に表現しています。
動くボールを描画する
動くボールを描画していきましょう。
先ほどまでで、ボールの情報が随時更新されていくようになったので、それをあとは描画していきます。
fn view(app: &App, model: &Model, frame: Frame) {
let draw = app.draw();
draw.background().color(BLACK);
draw.ellipse()
.x_y(model.px, model.py)
.radius(10.0)
.color(WHITE);
draw.to_frame(app, &frame).unwrap();
}これで、動く白いボールが描画できました。
このままだと、壁を通り抜けてどこまでも進んでいってしまいます。
ここから、本題の、跳ね返るボールを描画をやっていきましょう
跳ね返るボールを描画する
動くボールを描画することはできました。
あとは、このアルゴリズムに少し手を加えて、跳ね返るボールのアルゴリズムに書き換えていきます。
ボールが跳ね返るっていうことは?
ボールが跳ね返るっていうのを少し考えてみましょう。
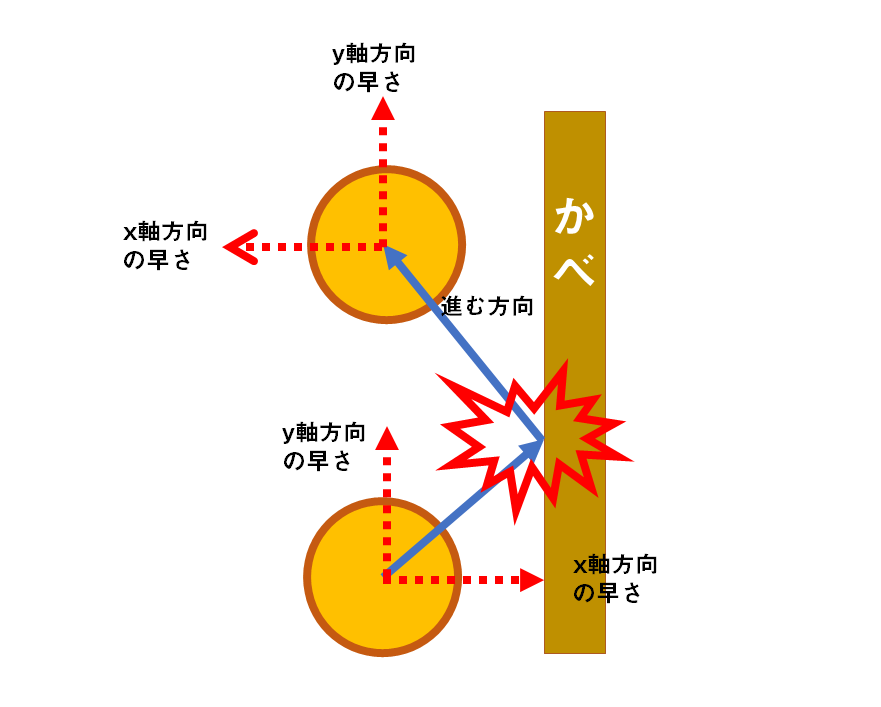
図にするとこんな感じです。
ヨコの壁にぶつかった時を考えてみると、y軸方向の向きは何も変化ありませんが、x軸方向の向きは逆になります。
同様に天井や床にぶつかるとx軸方向は変わらずにy軸方向の向きが逆になります。
向きが逆を座標で考えてみましょう。
右向きが正だとすると、左向きは負、右に進んでるものにマイナスを掛ければ負になって、左に進みます。
左に進んでるもの(進は速度はマイナス)にマイナスを掛けるとプラスになるので、右に進みます。
というわけでそれをプログラムしていきます。
跳ね返りをプログラムする
ここで手を加えるのはupdate関数の中だけです。
ソースから見ていきましょう
fn update(app: &App, model: &mut Model, _update: Update) {
let speed = 2.0;
let win = app.window_rect();
//跳ね返りの処理スタート
if model.py > win.top() || model.py < win.bottom() {
model.vy = -model.vy;
}
if model.px > win.right() || model.px < win.left() {
model.vx = -model.vx;
}
//跳ね返りの処理ここまで
model.px += speed * model.vx;
model.py += speed * model.vy;
}こんな感じです。
まずは、window_rect()を使ってウインドウサイズを取得します。
最初のif文が最初のが天井と床の跳ね返り、次のif文が左右の壁の跳ね返り
ボールの座標、pyがwin.top()より大きい(天井突き抜けちゃう)
もしくは(「||」もしくはの記号)
bottomより小さい(床突き抜けちゃう)ときは、vxを-vx(マイナス1倍)にしてください
っていうことが書いてあります。左右の壁も同様です。
ちなみに、model.vy=-model.vyっていうのをmodel.vy*=-1.0とかって書いても動きます。
nannouの場合はwindowの中心が原点になっているので条件式はこういう風に書きますが、例えばproceccingだと左上端が原点なので、座標の取り扱いはそれにあわせてください。
これで、ボールがどんどんどんどん跳ね返って描画されていきます。
まとめ
さて、今回は、rust nannouで動くボールの表現と跳ね返りのアルゴリズムをプログラムしました。
お気づきの方もいると思いますが、実はこれだと、ボールが壁にめり込んだりします(笑)
そこらへんは、ボールのサイズとかを考慮して、条件式を書き換えてみてください。
今回のプログラムは、跳ね返りは反発係数1の描画です。完全に跳ね返ります。
色々と、パラメーターを書き換えることで、例えば、上にぶつかったら少し速度が落ちるとか、逆に左にぶつかったら速度がアップするとか、そういうこともできるようになります。
あとは、ちょっと歪んで跳ね返るなんていうのもプログラムの描き方によっては表現できます。
さらに自由落下の法則の要素を加えることで、バウンドするボールとかもできます。
表現や利用シーンで色々書き換えれるので、今回を参考に取り組んでみてください
この発展形で構造体structと実装implを使って複数のボールを描画するっていう方法も解説してるので、いっぱいボール描きたいっていう方はそちらもあわせてどうぞ
ではまた!



コメント
[…] […]