Juliaでグラフをプロットする‐応用編2‐

今回は、応用編２ってことで、ちょっと教科書に載ってるようなグラフ書いてみようかなって思います。

今回はサクッと簡単な感じでやっていきますからお気軽に

基礎編や応用編１も併せてごらんください。

ではやっていきましょう！

実行環境
教科書みたいな正規分布を描く
まとめ

実行環境

このソースは、以下の環境で実行しています。

windows11
julia1.9.2
Distributions 0.25.100
StasPlots 0.15.6
Plots 1.38.17

教科書みたいな正規分布を描く

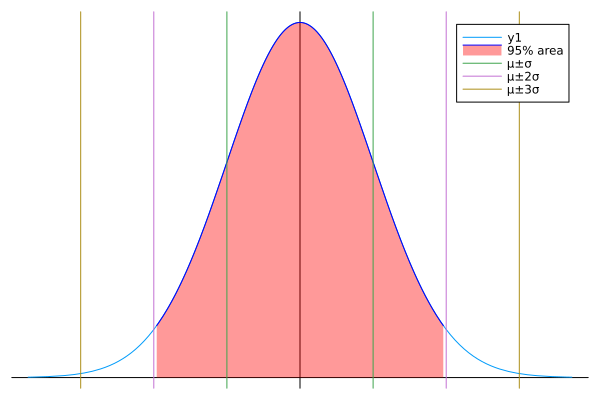
今回は、統計の基礎のところで、正規分布を習うとき、平均から分散の〇倍離れると・・・とかっていう図を見ると思います。あと、９５%は平均プラマイ1.96 なんちゃらーってのもやるよね。

それを合わせて、こんなグラフ書いていきます。

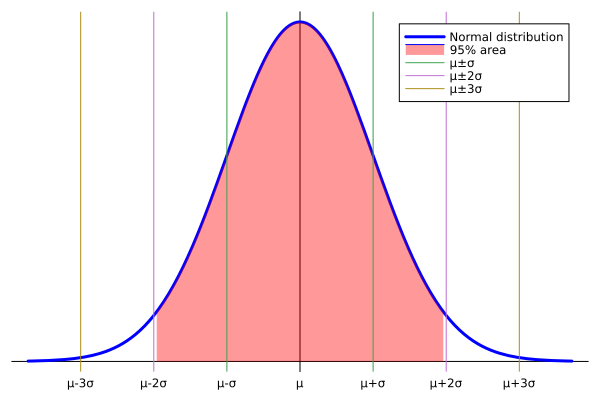
かっこいいでしょ

DistributionsとStasPlotsを使って正規分布を描く

まずは、正規分布描きましょう

using Distributions,StatsPlots,Plots
d1 = Normal()
plot(d1)

これで、まずは単純な正規分布が描けます。

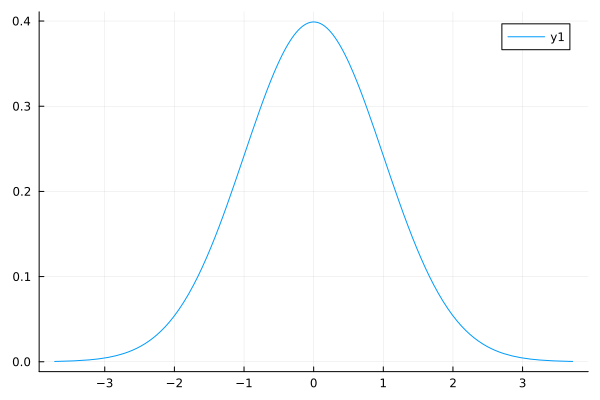
ここから加工していきます。

95%エリアを塗りつぶす

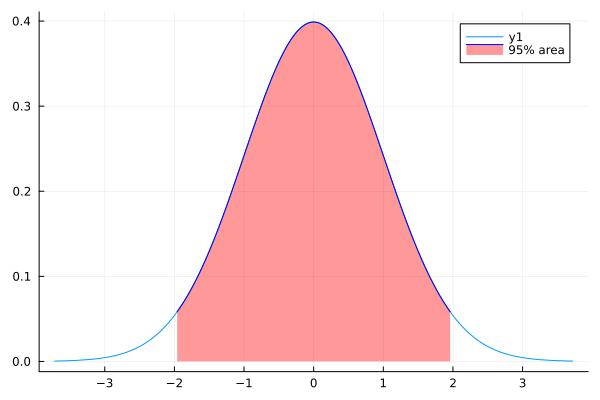
まずは95%エリアを塗りつぶしていきましょう。

plot(d1)
plot!(d1,mean(d1)-1.96*std(d1),mean(d1)+1.96*std(d1);fill=(0,0.4,:red),color=:blue,label = "95% area")

95%エリアは、平均プラマイ1.96σの範囲。

plot!(グラフ、範囲の下限、範囲の上限;塗りつぶしの条件、線の色、ラベル)って感じで指定してます。

fill=()の中身はfilrange,fillalpha,fillcolor

ちょっと薄く塗ってる感じだね。

vline!で縦の直線を描く

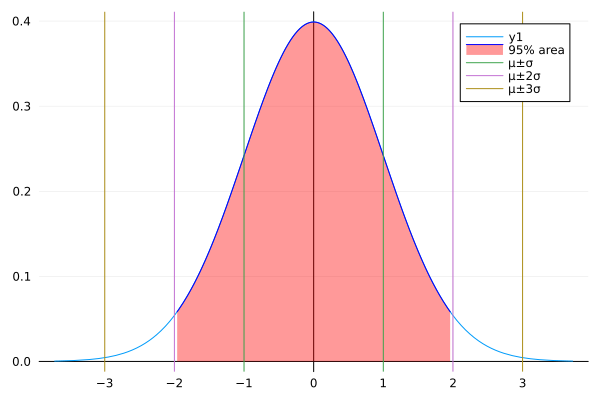
次に平均プラマイ〇分散の場所に縦線を付けていこう。

縦線はvline!()で描けるよ。引数はAbstractVectorで渡してね。

ちなみに横線はhline!()です。

vline!([mean(d1)-std(d1),mean(d1)+std(d1)],label="μ±σ",linewidth = 1)
vline!([mean(d1)-2*std(d1),mean(d1)+2*std(d1)],label="μ±2σ",linewidth = 1)
vline!([mean(d1)-3*std(d1),mean(d1)+3*std(d1)],label="μ±3σ",linewidth = 1)

ちゃんとラベルも付けよう。

そうするとこんな感じ

いい感じだね。

これで、だいたいグラフとして描画するものは出来上がり。

最後に見た目を整えていきましょう

見た目を整える

まずは、数値がふられたx軸とy軸、これはちょっとカッコ悪いよね。

教科書の図だと大体０が平均のところだよね。

最初のplot(d1…..)のところに

framestyle=:zerolinesって追加する

そうするとこうなる

次に目盛りだ、

まずは目盛りを消す。

ticks=:none

そして、それぞれの直線の下に自分独自の目盛りをふっていく

xticks!()ってのを使います。

目盛りの値とそれに対応するラベルをベクトルで渡します。

そうするとこうなる。

最後に線の太さやラベル名を微調整して出来上がり

出来上がりのコード全体はこんな感じです。

using Distributions,StatsPlots,Plots
d1 = Normal()
plot(d1,linewidth = 3,color=:blue,framestyle=:zerolines,ticks=:none,label="Normal distribution")
plot!(d1,mean(d1)-1.96*std(d1),mean(d1)+1.96*std(d1);fill=(0,0.4,:red),color=:blue,label = "95% area")
vline!([mean(d1)-std(d1),mean(d1)+std(d1)],label="μ±σ",linewidth = 1)
vline!([mean(d1)-2*std(d1),mean(d1)+2*std(d1)],label="μ±2σ",linewidth = 1)
vline!([mean(d1)-3*std(d1),mean(d1)+3*std(d1)],label="μ±3σ",linewidth = 1)
xticks!([mean(d1)-3*std(d1),mean(d1)-2*std(d1),mean(d1)-std(d1),mean(d1),mean(d1)+std(d1),mean(d1)+2*std(d1),mean(d1)+3*std(d1)],["μ-3σ","μ-2σ","μ-σ","μ","μ+σ","μ+2σ","μ+3σ"])